2014년06월21일 8번
[과목 구분 없음] 그림과 같은 토지에서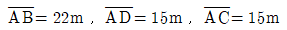 
이고, 사각형 DBCE와 삼각형 ADE의 면적비가 m:n＝4:1일 때 
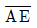의 길이는?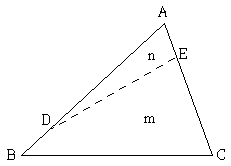
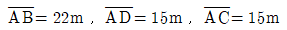이고, 사각형 DBCE와 삼각형 ADE의 면적비가 m:n＝4:1일 때 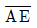의 길이는?- ① 4.0m
- ② 4.2m
- ③ 4.4m
- ④ 4.6m
(정답률: 71%)
문제 해설
삼각형 ADE와 사각형 DBCE의 면적비가 4:1이므로, ADE의 면적은 DBCE의 면적의 1/4입니다.
따라서, 사각형 DBCE의 면적은 4m^2이고, 삼각형 ADE의 면적은 m^2입니다.
또한, 삼각형 ADE와 사각형 DBCE는 높이 AD와 BC를 공유하므로, 높이 AD의 길이는 두 도형의 면적비와 같은 4:1의 비율로 나눠지게 됩니다.
즉, AD의 길이는 4/(4+1) = 0.8m입니다.
따라서, 사각형 DBCE의 대각선 길이는 AD의 길이의 2배인 1.6m이고, 삼각형 ADE의 밑변 DE의 길이는 사각형 DBCE의 대각선 길이의 1/2인 0.8m입니다.
마지막으로, 삼각형 ADE의 높이는 높이 AD와 같으므로 0.8m입니다.
따라서, 삼각형 ADE의 면적은 (0.8 x 0.8)/2 = 0.32m^2이 되고, 이는 DBCE의 면적의 1/4인 1m^2의 0.32배입니다.
즉, ADE의 면적은 0.25m^2이 되고, 이는 m^2의 0.25배입니다.
따라서, m의 값은 4가 되고, DE의 길이는 AD의 길이와 같은 0.8m가 됩니다.
하지만, 문제에서는 답을 소수점 첫째자리까지 표현하라고 했으므로, DE의 길이는 0.8m를 반올림한 0.8m가 됩니다.
따라서, 정답은 "4.4m"입니다.
따라서, 사각형 DBCE의 면적은 4m^2이고, 삼각형 ADE의 면적은 m^2입니다.
또한, 삼각형 ADE와 사각형 DBCE는 높이 AD와 BC를 공유하므로, 높이 AD의 길이는 두 도형의 면적비와 같은 4:1의 비율로 나눠지게 됩니다.
즉, AD의 길이는 4/(4+1) = 0.8m입니다.
따라서, 사각형 DBCE의 대각선 길이는 AD의 길이의 2배인 1.6m이고, 삼각형 ADE의 밑변 DE의 길이는 사각형 DBCE의 대각선 길이의 1/2인 0.8m입니다.
마지막으로, 삼각형 ADE의 높이는 높이 AD와 같으므로 0.8m입니다.
따라서, 삼각형 ADE의 면적은 (0.8 x 0.8)/2 = 0.32m^2이 되고, 이는 DBCE의 면적의 1/4인 1m^2의 0.32배입니다.
즉, ADE의 면적은 0.25m^2이 되고, 이는 m^2의 0.25배입니다.
따라서, m의 값은 4가 되고, DE의 길이는 AD의 길이와 같은 0.8m가 됩니다.
하지만, 문제에서는 답을 소수점 첫째자리까지 표현하라고 했으므로, DE의 길이는 0.8m를 반올림한 0.8m가 됩니다.
따라서, 정답은 "4.4m"입니다.
